Final Project - Neural Radiance Field
Filip Malm-Bägén

Introduction
This project is about implementing neural radiance fields (NeRFs) to reconstruct 3D scenes from 2D images by sampling and querying rays to integrate color information. The goal is to build efficient and robust methods for ray generation, sampling, and rendering to ensure high-quality results while minimizing overfitting.
Part 1: Fit a Neural Field to a 2D Image
The main task was to fit a neural field F that maps 2D
pixel coordinates {u, v} to RGB color values
{r, g, b}. To achieve this, I implemented a
Multi_Layer_Perceptron class with the following
architecture:
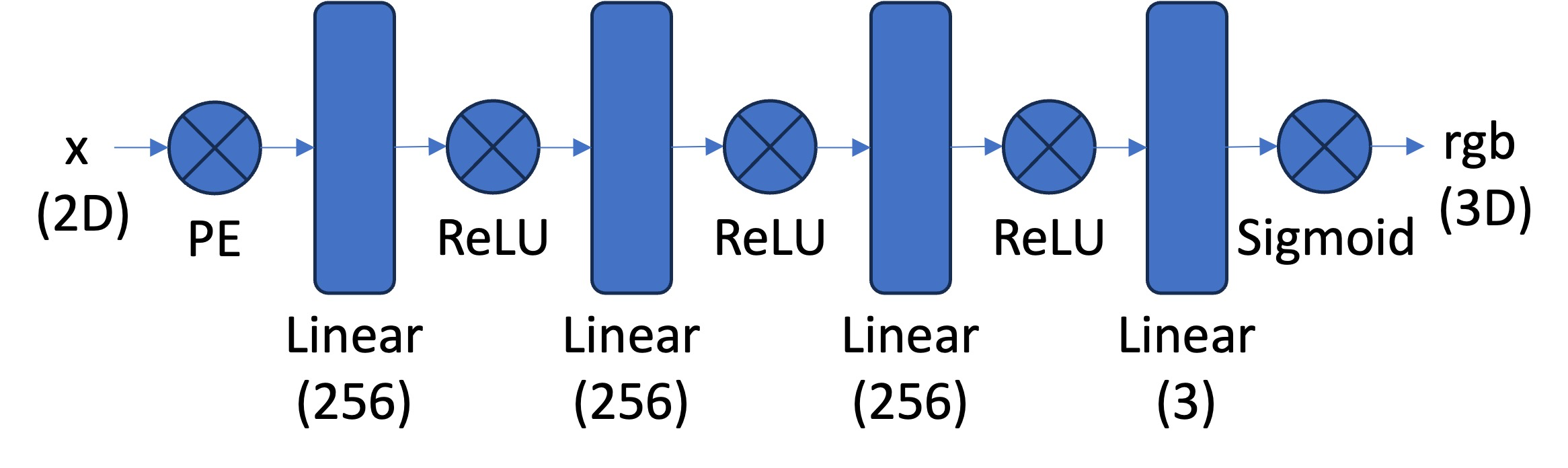
The inputs to the network were augmented using Sinusoidal Positional
Encoding (PE) using get_PE, which expands the input
dimensionality from 2 to 4 * L + 2 based on the
frequency level L. To train on large images, I had to
implement a dataloader class, RandomPixelSampler, which
samples N random pixels per iteration and returns both
their normalized coordinates and RGB values.
During the last step, I experimented with different hyperparameters to see how the results was effected. As seen in the images, the base configuration performed the best. The reduced frequency made the fox look more smooth and cartoonish. This is no surprise since the reduced frequency makes the network less sensitive to high-frequency details. The wider configuration and higher learning rate did perform the worst, as they resulted in black images. This result is also confirmed by the PSNR graph. However, this was not the case for the palace image, where the wider configuration performed the best. This is likely due to the increased complexity of the image.
| Configuration | Channel Size | Learning Rate | L |
|---|---|---|---|
| Base | 256 | 1e-2 | 10 |
| Reduced Freq | 256 | 1e-2 | 3 (Reduced frequency) |
| Wider | 512 (Double channel size) | 1e-2 | 10 |
| Higher LR | 256 | 1e-1 (Higher learning rate) | 10 |





The images represent iteration [1, 20, 100, 500, 1000, 2000]
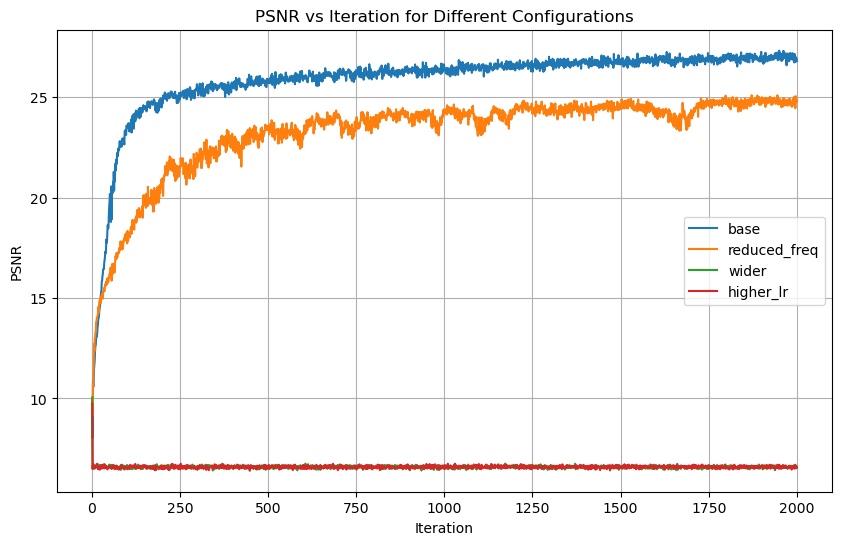





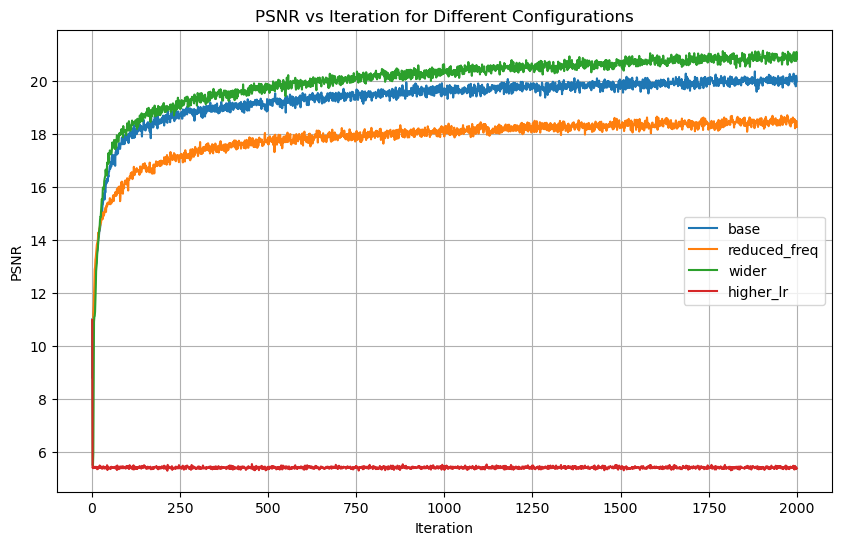
The reconstruction quality was evaluated using the Peak
Signal-to-Noise Ratio (PSNR), calculated as
PSNR = 10 * log10(1 / MSE)
Part 2: Fit a Neural Radiance Field from Multi-view Images
This part involves using a Neural Radiance Field (NeRF) to represent
a 3D scene by learning a mapping from position and view direction to
color and density:
F: {x, y, z, d} → {r, g, b, σ}. Using multi-view
calibrated images of a Lego scene (200x200 resolution) and their
corresponding camera poses, the task aims to perform inverse
rendering. The provided data includes camera-to-world matrices for
training, validation, and test cameras.
Part 2.1: Create Rays from Cameras
To render the 3D scene, I implemented functions to convert pixel
coordinates into rays, defined by their origin (ro) and normalized direction (rd). The coordinate transformations are performed and a function
transforms camera coordinates to world coordinates using the
camera-to-world matrix. Another function transforms pixel
coordinates to camera coordinates using the intrinsic matrix and
pixel depth. For ray generation, the ray origin is the camera's
translation vector, and the direction is computed by normalizing the
difference between the world coordinate of a depth-1 point and the
origin. These transformations are implemented using batched matrix
multiplications for efficiency.
Part 2.2: Sampling
Next, I developed ray sampling methods. I trained the model using a
batch size of 10k rays. These rays were generated by randomly
sampling 10k pixels globally across the training set of 100 images.
To accelerate the training process, all rays and pixel coordinates
were precomputed at the start. To render the 3D scene, each ray was
discretized into sampled points along its path. This step allows
querying points to integrate their colors for determining the final
color rendered at a particular pixel. Using uniform sampling, I
generated points along each ray as:
t = np.linspace(near, far, n_samples), where
near=2.0, far=6.0, and
n_samples=64. The 3D coordinates for these points were
calculated as: x = r_o + r_d * t, where
r_o represents the ray origin, and r_d the
ray direction. I added perturbations during training,
t = t + np.random.rand(t.shape) * t_width. This ensures
that all locations along the ray are touched.
Part 2.3: Putting the dataloader all together
I ran the code to verify that I had implement everything correctly.

Part 2.4: Neural Radiance Field
The Neural Radiance Field was implemented as a deep neural network that maps spatial coordinates and viewing directions to color and density values. This network was enhanced to handle higher-dimensional inputs (3D position and view direction vectors) and outputs (RGB colors plus density), compared to the MLP from part 1. The complete network architecture is illustrated below:
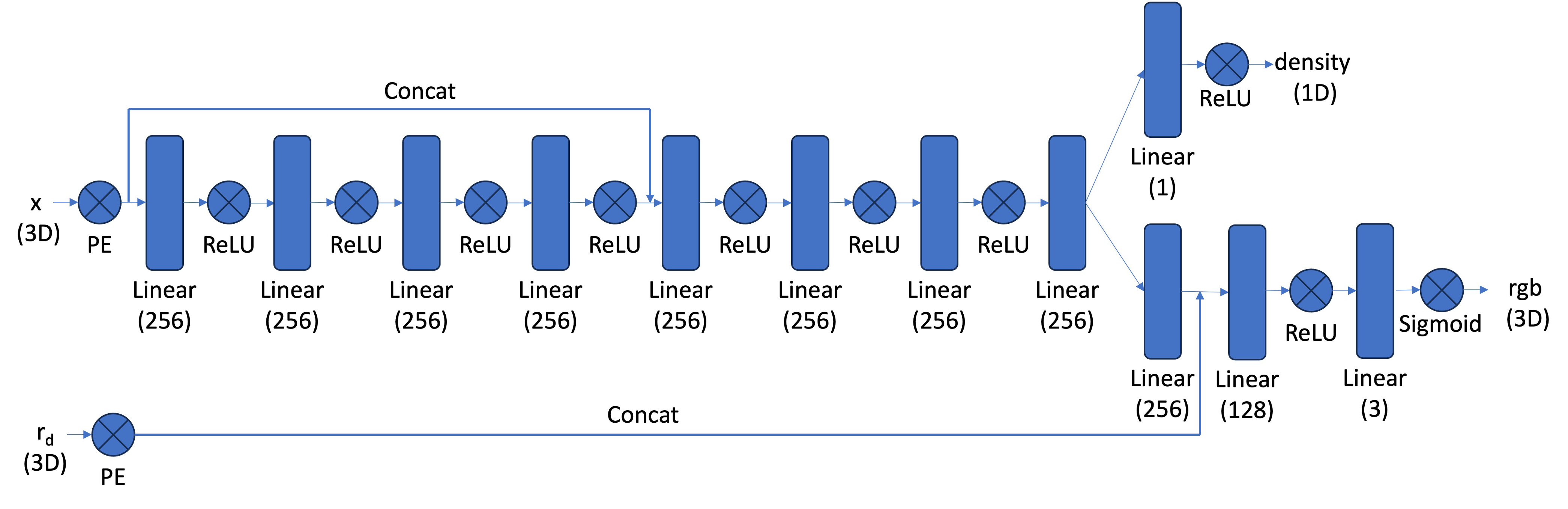
Part 2.5: Volume Rendering
Volume rendering integrates color values along each ray to produce the final pixel color. At each sampled point along a ray, the network predicts both color and density values. These values are then combined using a numerical approximation of the volume rendering equation. The rendering process works by accumulating colors from back to front along each ray, using density values (σ) to determine opacity at each point, weighting colors based on transmittance (how much light passes through), and computing distance intervals (δᵢ) between sampled points.
The implementation uses PyTorch's torch.cumprod for
efficient calculation of transmittance values. The distance
intervals δᵢ are derived from the sampling points generated earlier
in the pipeline. This numerical approximation enables efficient
parallel computation across all rays in a batch.
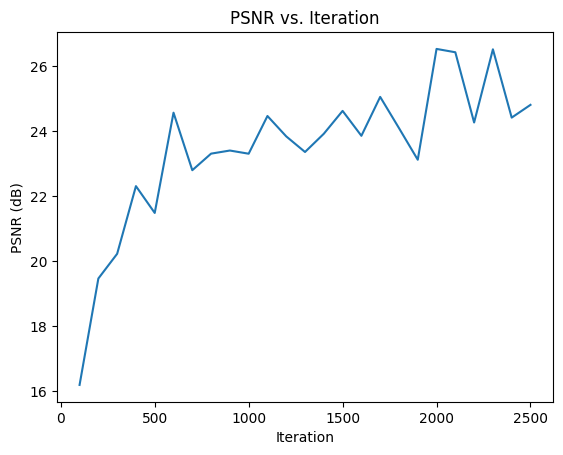
I trained using Adam optimizer with
learning_rate = 1e-3,
batch_size = 10_000 and iterations = 2500.
The images below are visualizations of the training process.








The following image is the PSNR curve over the iterations. The PSNR is steadily increasing, and I believe that the model could acieve a PSNR greater than 30 if trained for more iterations.
The final image is the rendered image of the Lego scene. The rendering quality is quite good, and the model has learned to represent the scene well. Next to it is the depth image, which represents the distance from the camera to the object. The darker the pixel, the closer it is to the camera. The difference is that the depth rendering only uses the density value, while the color rendering uses both the color and density values.


This webpage design was partly made using generative AI models.